Introducing DARA: A New Design for ZK Prover Networks

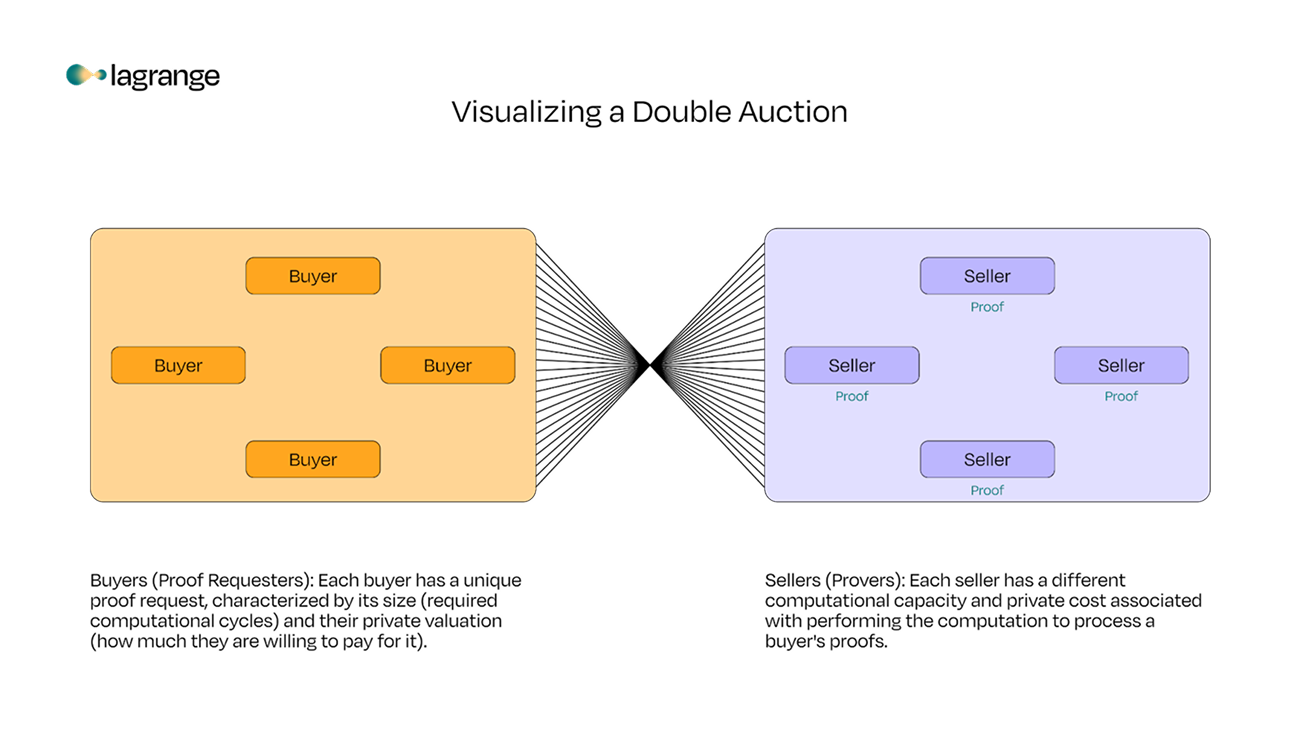
As zero-knowledge (ZK) proofs become more critical to the scaling and verifiability of blockchain ecosystems, the demand for efficient methods of matching those who need computational resources with those who can provide them has never been higher. Traditional single auction mechanisms, where there is one seller and many buyers, fall short for proof marketplaces, where there are many buyers (those seeking compute resources to generate ZK proofs, AKA “proof requesters”) and sellers (those providing the compute power for proving, AKA “provers”), which require a double auction mechanism. In a double auction for prover networks, the auctioneer’s job is to find the optimal match between proof requesters and provers, determining which proof requesters get their bids accepted and which provers provide the proofs, all while setting fair prices for both sides.

Lagrange's latest research introduces DARA, the first incentive-aligned Double Auction Resource Allocation mechanism for prover networks that hits the sweet spot between optimizing costs for proof requesters, maximizing revenue for provers, and ensuring the marketplace operates fairly and profitably.

The Challenge

Up until now, proving marketplaces have struggled with the challenge of allocating resources (supply and demand of the marketplace) in a way that maximizes efficiency, affordability for proof requesters, and profitability for provers. In other words, existing prover networks are plagued by an incentive-alignment problem. Matching proof requesters and provers efficiently is challenging because both parties have their own preferences: proof requesters want to minimize their cost while provers want to maximize their revenue. Furthermore, ZK proofs are computationally expensive, and some proofs require a fixed number of compute cycles. This creates an all-or-nothing constraint, meaning a proof-requester either gets all the computational resources they need or derives no value from partial allocation.

The key questions for any proof marketplace are:

• How can we allocate proving resources in a way that maximizes total welfare for all participants?
• How can the market incentivize truthful bidding and pricing to avoid inefficient matches?
• How can we ensure the auction is sustainable so that the protocol (auctioneer) doesn’t lose money?

The Solution

DARA, developed by Lagrange, provides an innovative solution to this challenge by introducing a knapsack double auction mechanism specifically designed to tackle the complexities of decentralized proof markets. This breakthrough ensures that both provers and proof requesters benefit from an efficient, scalable, and fair mechanism. DARA achieves the five requirements for a fair and efficient auction system: welfare-maximization, truthfulness, weak group-strategy proofness, weak budget-balance and computational efficiency.

How it Works

DARA hits the sweet spot between optimizing costs for proof-requesters, maximizing revenue for provers, and ensuring the marketplace operates fairly and profitably. Here’s how DARA works:

Welfare Maximization: Matching Proof Requesters and Provers Efficiently

DARA optimizes for both sides of the market, maximizing the welfare of both proof-requesters and provers. Proof-requesters submit their requests, specifying how many computational cycles they need and their private value for completing the proof. Provers submit their available compute capacity and private value per compute cycle. Both buyers and sellers are then ranked based on their private values with an algorithm that favors higher-value bids (from proof-requesters) and lower-cost per cycle of compute (from provers). With these rankings, DARA matches as many buyers and sellers as possible, ensuring that the most efficient matches are made.

The knapsack constraint further ensures that each proof requester is only considered if their entire request can be fulfilled—partial allocations for buyers aren't valuable, so it's an all-or-nothing scenario. This means that a proof requester who needs 10,000 compute cycles can only be matched with provers who can collectively offer at least 10,000 cycles. In this same logic, provers can be partially allocated to multiple buyers if they have the total capacity to fulfill multiple requests.

Truthfulness: Incentivizing Proof-Requesters and Provers to Share their Private Values

Instead of inflating costs due to unpredictable demand, DARA ensures that truthful bidding is the best strategy for both proof requesters and provers. The mechanism uses a threshold payment system to ensure that a) proof requesters only pay what is necessary to win the computation they need and b) provers maximize their profitability in a truthful auction. Proof-requesters are charged based on the minimum amount they need to pay to secure their place in the auction (preventing them from being overcharged), whereas provers are compensated fairly based on the costs of other provers in the market (incentivizing them to offer competitive pricing).

For example, consider a ‘simplified’ case where each proof is a single unit of computation. Suppose there are five proof requesters who want their proofs computed with the respective private values of $5.00, $6.00, $7.00, $8.00, and $9.00 (what they are willing to pay for computation). On the other hand, there are also five provers—with one unit of compute capacity each—with the respective private values of $3.00, $4.00, $5.00, $6.00, and $7.00 (the price they are willing to compute proofs for). In this setting, we can retain truthfulness by finding the threshold value v where there are k proof requesters with a private value greater than or equal to v and k provers with a private value less than or equal to v. In our example, this is $6.00 (note: the threshold does not necessarily need to be the value of a specific bid). In this case, there are four proof requesters willing to transact for $6.00 dollars and similarly four provers. In order to maximize the welfare, we can set the proof cost to $6.00 and accept the the last four proof requesters and the first four provers. This ‘simplified’ example speaks to the complexities of double auctions. In our real-world setting, things get trickier with the addition of multi-sized proofs, so the matching algorithm must be modified to suit them (specifically we might have small requests with large value per cycle and large requests with smaller value per cycle but larger total value, and it is not clear exactly how to rank these)—however, this ‘simplified’ case gives some intuition as to the logic behind achieving truthfulness in a double auction bid. 

This threshold payment system is particularly important in ZK proof markets, where computational costs can be high and buyers need to optimize their spending to stay competitive. Truthful bidding helps build a marketplace where Lagrange can effectively allocate the proofs to those who care about them the most, for a fair price. Furthermore, since alternative strategies are not effective (since truthful bidding is the best strategy), DARA allows small players and big players alike to participate fairly.

Weak-Group Strategy-Proofness (Anti-Collusion)

We have seen that in DARA, any single party (either a proof-requester or prover) has no incentive to lie about their private valuation. If they underbid, they may lose the auction altogether, and if they overbid, they risk paying more than necessary or receiving less compute than needed. Furthermore, groups of proof-requesters and provers have no incentive to attempt at strategizing together to improve their auction outcomes. In this sense, DARA is weak group-strategy proof, meaning that even if a group of participants tries to collude to manipulate the outcome of an auction, at least one member of the group will find it more profitable to bid truthfully, preventing the auction from being skewed by collusion. This helps mitigate collusion attacks by making them unprofitable for at least one person.

Computational Efficiency: Scale, Scale, Scale!

One of the standout features of the knapsack double auction is its computational efficiency. Unlike other auction models that may be computationally intensive or impractical for large-scale decentralized systems, DARA operates in polynomial time, achieving near-linear complexity (the number of participants grows at a linear scale). This means that DARA can scale effectively, even as the number of buyers and sellers grows, ensuring that the proof marketplace can handle increasing demand without bottlenecks or excessive delays. The efficient design allows the system to match multiple participants simultaneously, optimizing resource distribution without compromising on speed or accuracy.

Weak Budget Balance & Sustainability for the Protocol

DARA ensures that the protocol (acting as the auctioneer) does not lose money while facilitating the auction. In traditional resource allocation systems, the protocol might subsidize transactions, leading to unsustainable financial models. DARA, however, ensures that the protocol only accepts bids for proof computation higher than the cost of proving, which means that the protocol will never have to subsidize transactions at a loss. This ensures that the protocol remains financially neutral (it neither loses nor gains money from the auction process) and can sustain the auction indefinitely.

Impact on Proof Marketplaces

DARA has far-reaching implications for decentralized proof marketplaces. By balancing affordability, truthfulness, and scalability, DARA empowers proof marketplaces to operate more effectively and maximizes incentives for all participants. Here’s how:

• For Proof-Requesters (Buyers): Decentralized protocols that rely on frequent ZK proofs can benefit from a marketplace where they only pay the minimum necessary cost to secure the computation they need. This reduces their operational expenses and allows them to implement more complex use cases that leverage ZK proofs, such as privacy-preserving smart contracts and scalable rollups.
• For Provers (Sellers): Distributed proving nodes can maximize their profitability by efficiently selling their compute capacity without worrying about market manipulation or collusion. The auction system ensures they get a fair return on their investment, making proving networks more sustainable and competitive.
• For the Auctioneer (Protocol): The marketplace itself is sustainable and profitable. By ensuring that the auctioneer doesn’t lose money facilitating the auctions (weak budget balance), the system can be maintained and scaled without relying on subsidies or external funding to operate.

A New Kind of ZK Prover Network with Lagrange

DARA sets a new standard for resource allocation for decentralized prover networks. By aligning the interests of proof requesters and provers, ensuring truthfulness, and operating efficiently, it enables a truly incentive-aligned marketplace, something which was not previously possible. As the demand for ZK proofs continues to increase to support the needs of rollups and verifiable computation—Lagrange’s ZK Prover Network, powered by DARA, offers a scalable and efficient solution to scaling ZK and decentralized applications. Read the full research paper on DARA here.