A Big Data Primer: Introducing ZK MapReduce
May 25, 2023

The future of cross-chain interoperability will be built around dynamic and data-rich relationships between multi-chain dapps. Lagrange Labs is building the glue to help securely scale zero-knowledge proof based interoperability.

The ZK Big Data Stack:
The Lagrange Labs ZK Big Data stack is a proprietary proof construction optimized for generating large scale batch storage proofs concurrently with arbitrary dynamic distributed computation. The ZK Big Data stack is extensible to any distributed computational frameworks, ranging from MapReduce to RDD to distributed SQL.
With the Lagrange Labs ZK Big Data stack, a proof can be generated from a single block header, proving both an array of historical storage slot states at arbitrary depths and the results of a distributed computation executed on those states. In short, each proof combines both the verification of storage proofs and verifiable distributed computation, within a single step.
In this article, we’ll be discussing ZK MapReduce (ZKMR), the first product in the Lagrange ZK Big Data stack.
Understanding MapReduce:
In a traditional sequential computation, a single processor executes an entire program following a linear path, where each instruction is executed in the order that it appears in the code. With MapReduce and similar distributed computing paradigms such as RDD, the computation is divided into multiple small tasks that can be executed on multiple processors in parallel.
MapReduce works by breaking down a large dataset into smaller chunks and distributing them across a cluster of machines. Broadly, this computation follows three distinct steps:
- Map: Each machine performs a map operation on its chunk of data, transforming it into a set of key-value pairs.
- Shuffle: The key-value pairs generated by the map operation are then shuffled and sorted by key.
- Reduce: The results of the shuffle are passed to a reduce operation, which aggregates the data and produces the final output.
The main advantage of MapReduce is its scalability. Since the computation is distributed across multiple machines, it can handle large-scale datasets that would be infeasible to process sequentially. Additionally, the distributed nature of MapReduce allows computation to scale horizontally across more machines, rather than vertically in terms of computation time.
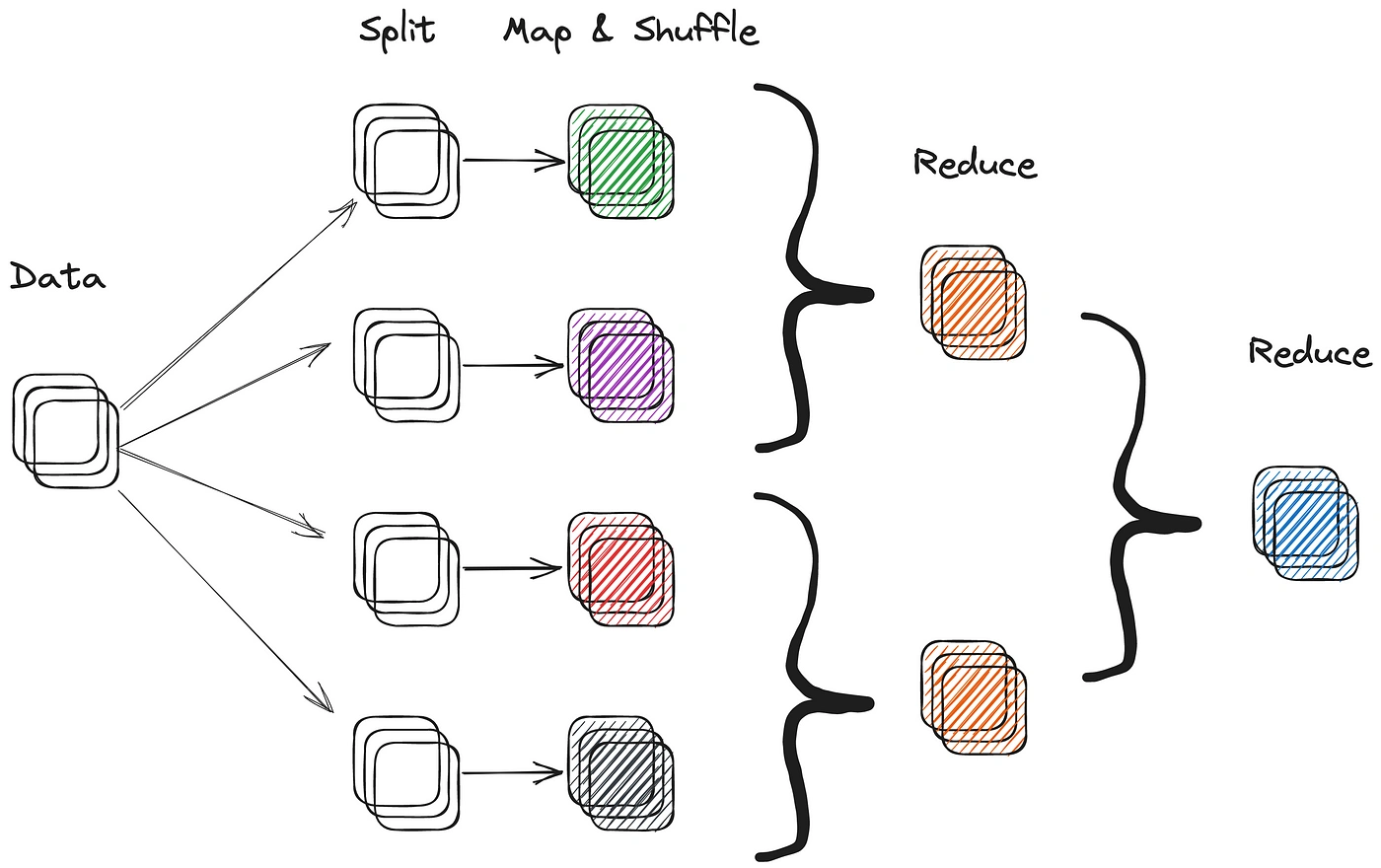
Distributed computation paradigms such as MapReduce or RDD are commonly used in Web 2.0 architectures for processing and analyzing large datasets. Most large web 2.0 companies, such as Google, Amazon and Facebook, heavily leverage distributed computation to process petabyte scale search data and user data sets. Modern frameworks for distributed computation include Hive, Presto & Spark.
An Intro To ZK MapReduce:
Lagrange’s ZK MapReduce (ZKMR) is an extension of MapReduce that leverages recursive proofs to prove the correctness of the distributed computation over large amounts of on-chain state data.This is achieved by generating proofs of computational correctness for each given worker during either the map or reduce steps of a distributed computation job. These proofs can be composed recursively to construct a single proof for the validity of the entire distributed computational workflow. In other words, the proofs of the smaller computations can be combined to create a proof of the entire computation.
The ability to compose multiple sub-proofs of worker computation into a single ZKMR proof enables it to scale more efficiently for complex computations on large data sets.
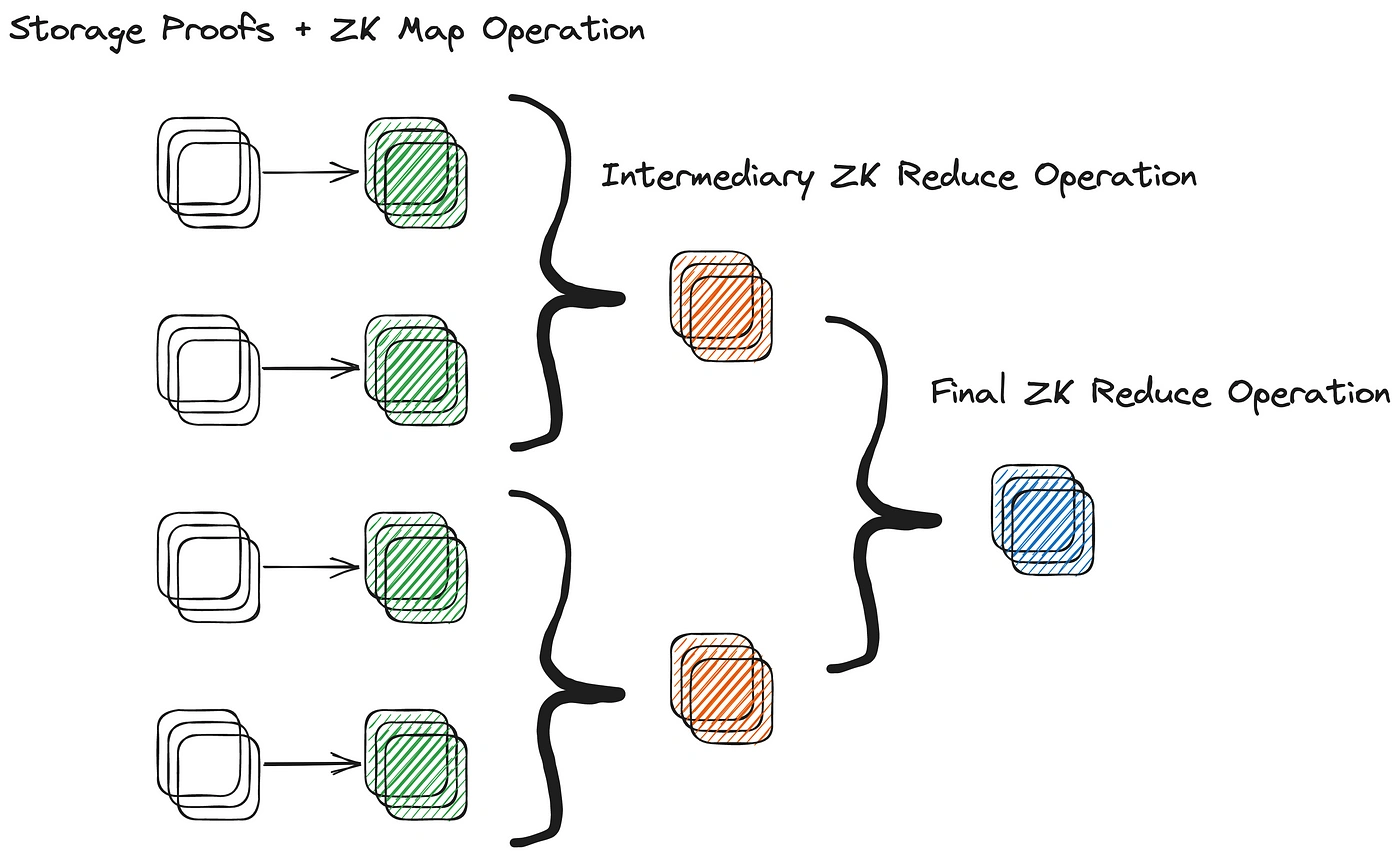
One of the principal advantages of ZKMR, as compared to zero-knowledge virtual machines (ZKVMs), is the ability to execute dynamic computations on top of present and historical contract storage state. Rather than having to prove storage inclusion across a series of blocks separately and then prove a series of computations on top of the aggregated data set, ZKMR (and other Lagrange ZK Big Data products) support composing both into a single proof. This significantly reduces proving time for generating ZKMR proofs, as compared to alternative designs.
ZK MapReduce In Action:
To understand how recursive proofs can be composed, let’s consider a simple example. Imagine that we want to calculate the average liquidity of an asset pair on a DEX over a given period of time. For each block, we must show the correctness of an inclusion proof on the state root, proving how much liquidity is in that DEX. Next, we must sum up all of the liquidity across every block in the average and divide it by the number of blocks.
Sequentially this computation would look as follows:
# Sequential Execution
func calculate_avg_eth_price_per_block(var mpt_paths, var liquidity_per_block){
var sum = 0;
for(int i=0; i<len(liquidity_per_block); i++){
verify_inclusion(liquidity_per_block[i], mpt_path[i])
sum += liquidity_per_block[i]
}
var avg_liquidity = sum / num_blocks
// return the average liquidity
return avg_liquidity
}
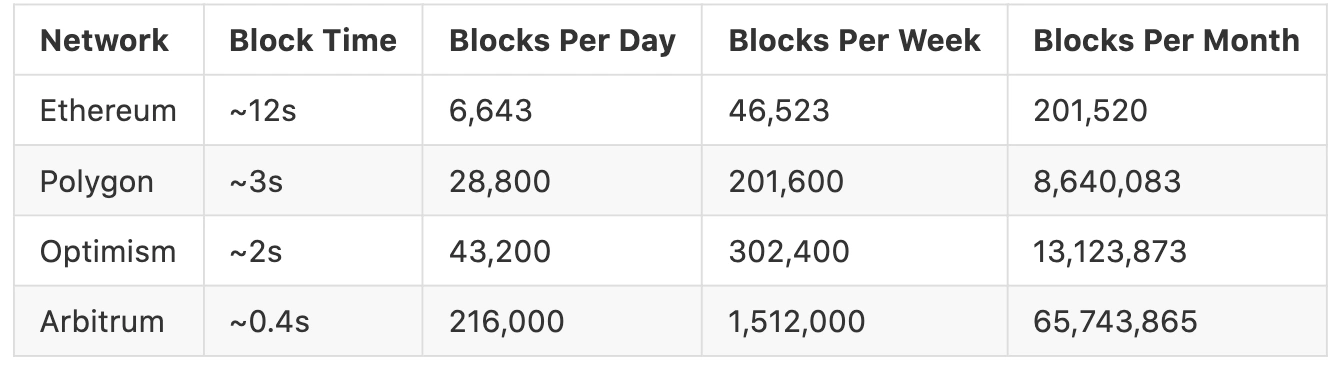
While this computation may intuitively appear straight forward, the performance degrades quickly as the amount of state that needs to be included increases. Consider the below table, showing the number of blocks per chain over specific time frames. At the limit, calculating the average liquidity in a single DEX on Arbitrum over 1 month would require data from over 65 million rollup blocks.
In contrast with ZKMR, we can divide the dataset into smaller chunks and distribute them across multiple processors. Each machine will perform a map operation that calculates the Merkle-Patricia Trie (MPT) proof and sum the liquidity for its chunk of data. The map operation then generates a key-value pair where the key is a constant string (e.g., average_liquidity) and the value is a tuple containing the sum and count.
The output of the map operation will be a set of key-value pairs that can be shuffled and sorted by key, and then passed to a reduce operation. The reduce operation will receive a key-value pair where the key is average_liquidity and the value is a list of tuples containing the sum and count of the liquidity from each map operation. The reduce operation will then aggregate the data by summing the individual sums and counts, and then dividing the final sum by the final count to get the overall average liquidity.
# Map step
func map(liquidity_data_chunk,mpt_path_chunk){
var sum = 0
for(int i=0; i<len(liquidity_data_chunk); i++){
verify_inclusion(liquidity_data_chunk[i], mpt_path_chunk[i])
sum += liquidity_data_chunk[i]
}
return ("average_liquidity", (sum, len(liquidity_data_chunk)))
}
# Reduce step
func reduce(liquidity_data_chunk){
var sum = 0
var count = 0
for(int i=0; i<len(liquidity_data_chunk); i++){
sum += value[0]
count += value[1]
}
return ("average_liquidity", sum/count)
}
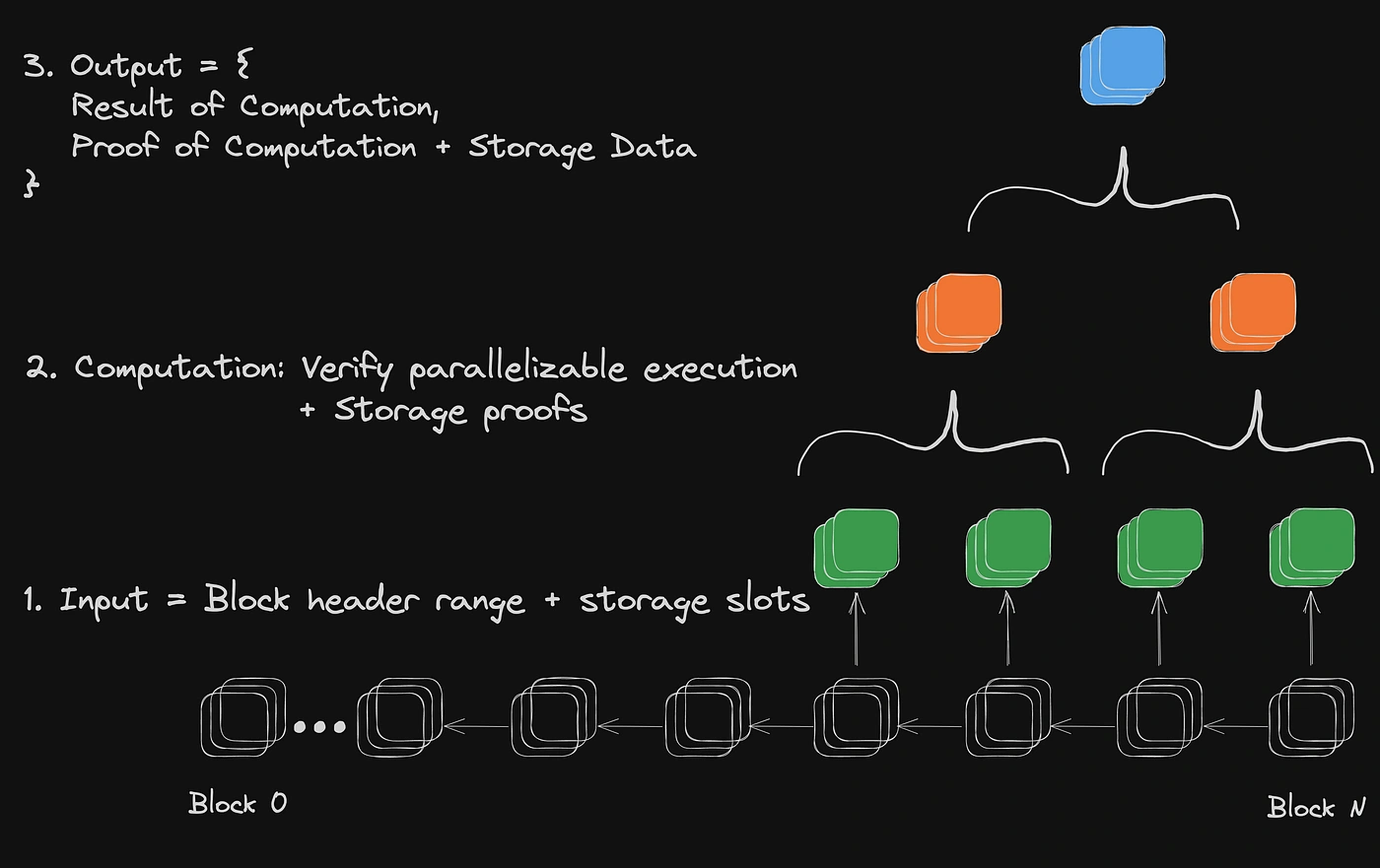
Broadly speaking, we can generalize the process of defining and consuming a ZKMR proof for a developer into three steps:
- Defining Dataframe & Computations: A ZKMR proof is executed with respect to a dataframe, which is a range of blocks and specific memory slots within those blocks. In the above example, the dataframe would be a range of blocks that the liquidity is averaged over and the memory slot corresponding to the asset’s liquidity in a DEX.
- Proving of Batched Storage & Distributed Computation: A ZKMR proof verifies the results of computations performed on a specific dataframe input. Each dataframe is defined with respect to a specific block header. As part of verifying computation, each proof must prove both the existence of underlying state data and the result of the dynamic computation run on top of it. In the above example, this would be an averaging operation.
- Proof Verification: A ZKMR proof can be submitted and verified on any EVM compatible chain (with more virtual machines supported soon).
Transport Layer Agnostic Proofs:
One of the powerful features of ZKMR proofs (and other ZK Big Data proofs) is their ability to be transport layer agnostic. Since the proofs are generated with respect to an initial block header input, any existing transport layer can opt into generating and relaying them. This includes messaging protocol, oracles, bridge, watchers/cron jobs and even untrusted or incentivized user mechanisms. The flexibility of ZKMR proofs enables them to drastically increase the expressivity of how state is being used between chains, without having to compete with existing and highly performant transport infrastructures.
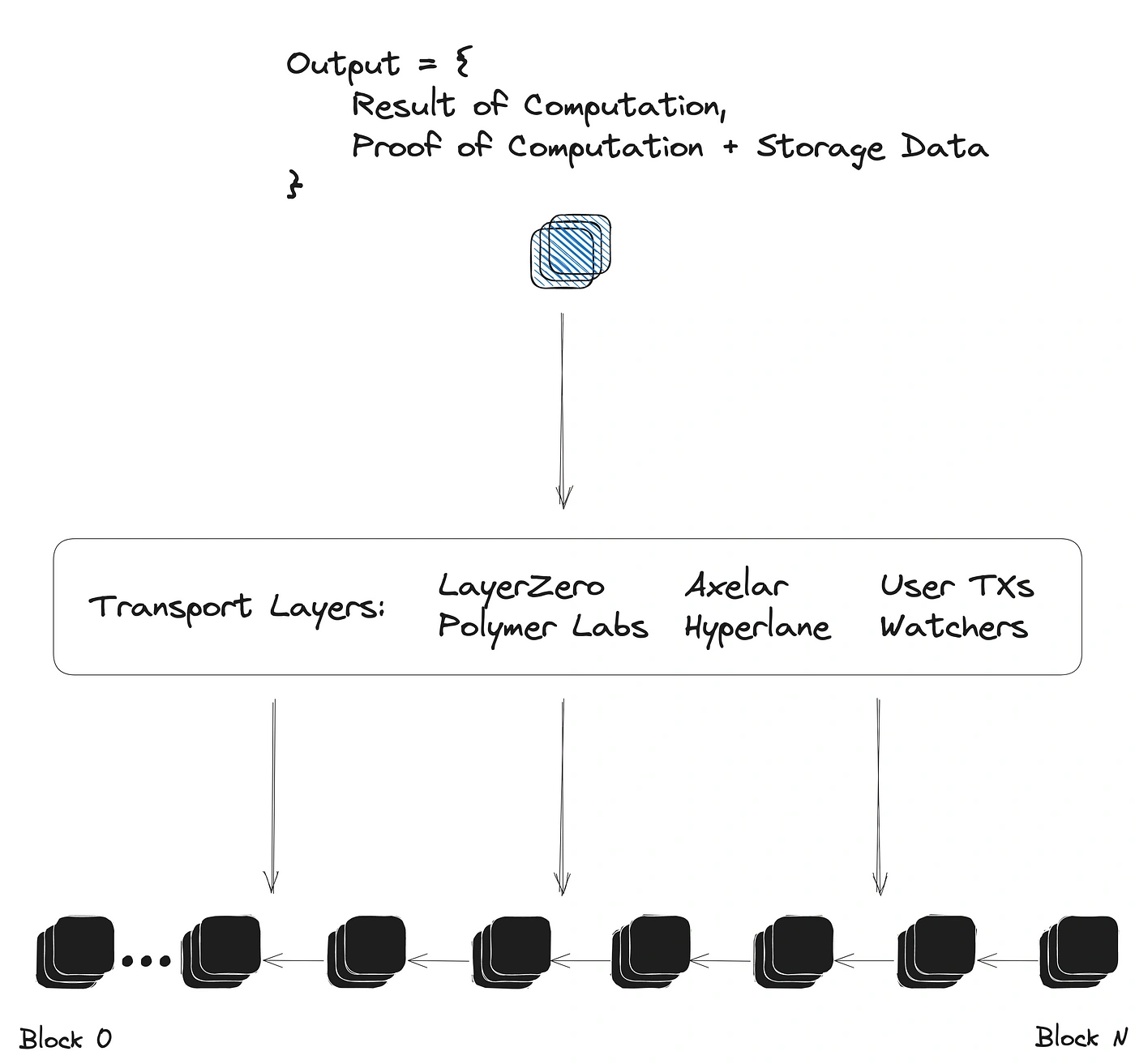
The Lagrange SDK provides an easy interface for integrating ZK Big Data proofs into any existing cross-chain messaging or bridging protocol. With a simple function call, a protocol can easily request a proof for the result of arbitrary computations on a specific dataframe contained within a given block header..
When integrating with an existing protocol, ZKMR is not designed to make assertions over the validity of the block headers used as input for the proofs. The transport protocol can prove or assert the validity of a block header as it typically would when passing a message, but can additionally now include dynamic computation on top of a dataframe of historical states.
It is worth noting that ZKMR proofs also support combining proofs from multiple chains into a single final computation.
Efficiency Improvements of ZKMR:
While the ZKMR approach may seem more complicated than traditional sequential computation, its performance scales horizontally with respect to the number of parallel processes/machines rather than vertically with respect to time.
The time complexity of proving a ZK MapReduce procedure is O(log(n)) when run with maximum parallelization, as opposed to the sequential execution which has a run-time of O(n).
As an example, consider taking the average liquidity taken across 1 day of Ethereum block data. Sequential execution would require a loop with 6,643 steps. The distributed approach with recursive proofs would instead require a single map operation with up to 6,643 parallel threads followed by 12 recursive reduction steps. This is a ~523x reduction in run-time complexity.
As we continue to fragment state storage across scalability solutions, such as app chains, app rollup L3s and alt-L1s, the amount of on-chain data being created is only growing and fragmenting exponentially. The question may very soon become, how much data will one have to process to compute a 1-week TWAP across a DEX deployed on 100 different app rollups?
In summary, ZKMR is a powerful paradigm for processing large-scale datasets in a zero-knowledge context across distributed computing environments. While sequential computation is highly efficient and expressive for general purpose application development, it is poorly optimized for analysis and processing of large data sets. The efficiency of distributed computing has made it the go to standard for much of the big data processing that has predominated Web2. In a zero-knowledge context, scalability and fault tolerance make it the ideal backbone for handling trustless big data applications, such as complicated on-chain pricing, volatility and liquidity analyses.
Contact Us:
Want to learn more about Lagrange?
Visit our website at https://lagrange.dev and follow us on Twitter at @lagrangedev to stay up to date.






